Everybody seems to be finding hidden messages from above these days. I see
that a piece of grilled cheese toast with the supposed burnt image of Christ
on it went for a fortune on Ebaytm recently. Now there is a very
popular bestseller out there analyzing Da Vinciís Last Supper, proposing that Jesus married Mary Magdalene -- and that his blood still runs
in the veins of European royalty. Only slightly before that, I read where the
Torah was found to contain spot-on, modern prophetic messages when its characters were
rearranged in modulo table fashion. Jeez, Iím really starting to feel
left out here.
My idea is that anybody can find his own hidden message if he looks
hard enough. Why not me? With my unique talent for focusing neurotically on
insignificant things, I certainly ought to be able to tease out a message
around here somewhere.
I decided to look for my own message within one of my long-time favorite
areas of interest, prime number theory. Iíve been fascinated by prime numbers
since I was 11 years old -- and still am. Primes, you will recall, are whole
numbers which are equally divisible only by themselves and the number 1. Starting from
1 and counting up, primes are discovered at 2, 3, 5, 7, 11, 13, 17,
19, 23, etc. All the other numbers in between are divisible by one of the earlier numbers
counted; these are called factors of that non-prime number. You can
break down those factors (by finding their own sub-factors, if they have any)
into a collection of lower-value factors. These are always prime numbers
themselves, and are known as prime factors. But a prime number has no
factors at all, except for itself and the number 1. (You can argue
whether or not the number 1 is a prime number. I've treated it somewhat
inconsistently here -- but that won't detract from my exposition.)
(If you take a couple of really large prime numbers and multiply them
together, you get a huger number that is extremely difficult to factor, even
by a powerful computer. This difficulty in factoring big numbers made up
of two large primes is the
basis of all modern encryption -- the thing that keeps people from stealing
your credit card number when you make an online transaction.)
Being an extremely visual-type person, I like to see the primes in a
graphical way. For example, suppose I draw little boxes in a row, each box
representing a counting number, and paint in the ones which are prime, like
so:

Of course, when you do this you run out of page width quickly. What I can
do is to select a certain width value, so the sequential numbers can wrap
around and begin again on the next row.
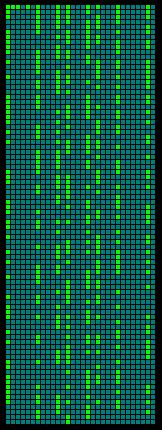 Now, it turns
out that if you make this value a multiplicand of the first several primes
(say, 30, which equals 2 X 3 X 5), an interesting thing happens Ė well,
interesting to me at least. See the image to the left. You will find
that most of the columns donít contain any primes at all. These are "dead"
columns, and with some thought itís easy to understand why. Every cell under
each of the even-numbered columns contain numbers that that are divisible by
2. The numbers under every 3rd column are divisible by 3.
Everything in every 5th column is divisible by 5. But some of the
columns donít have this property. When you get to column number 7, 11, 13, 17,
19, 23 and 29, the numbers underneath them may or may not be divisible by the
top number. (You can make those columns "dead" also, by including their initial
prime number in your total table width calculation; for example, width 210 = 2 X 3 X
5 X 7 will make every 7th column a "dead" one.)
Now, it turns
out that if you make this value a multiplicand of the first several primes
(say, 30, which equals 2 X 3 X 5), an interesting thing happens Ė well,
interesting to me at least. See the image to the left. You will find
that most of the columns donít contain any primes at all. These are "dead"
columns, and with some thought itís easy to understand why. Every cell under
each of the even-numbered columns contain numbers that that are divisible by
2. The numbers under every 3rd column are divisible by 3.
Everything in every 5th column is divisible by 5. But some of the
columns donít have this property. When you get to column number 7, 11, 13, 17,
19, 23 and 29, the numbers underneath them may or may not be divisible by the
top number. (You can make those columns "dead" also, by including their initial
prime number in your total table width calculation; for example, width 210 = 2 X 3 X
5 X 7 will make every 7th column a "dead" one.)
These "live" columns are where the primes reside. You can see that there
are also lots of primes under the "1" column. Looking at it from this perspective, I would make the case that the number 2, 3, and 5 are
really "faulty" primes in this particular arrangement. They just get included
because they came really early in the prime "test", and their "dead" column
status comes as a consequence of them being a party to establishing the total
width of the row.
from this perspective, I would make the case that the number 2, 3, and 5 are
really "faulty" primes in this particular arrangement. They just get included
because they came really early in the prime "test", and their "dead" column
status comes as a consequence of them being a party to establishing the total
width of the row.
I say ignore all the columns that donít have any primes appearing after the
first row, including the columns headed by those wimpy primes 2, 3 and 5. All
they do is detract from the pattern. We can then collapse the good fruitful
columns so that they are right next to each other. See the image to the right.
This really densifies all the primes and we get a much more interesting total
pattern. Trouble is, now weíre running out of room too soon on the page
height! I suppose we could just increase the original table width to make the
whole table more square, but instead, why donít we do what we did to the row
length: start wrapping the columns around when they get down near the bottom
of the page. So we continue to plot our (in this case) 8-column table,
bringing it up and positioning it next to and to the right of the first column
plots.
Eventually, we will end up with a
nice square page-filling table showing the primes lit up. Is it a random
pattern? Doesnít look like it to me. There are tantalizing hints of patterns
and small sub-patterns that seem to be in there. If I take off my reading
glasses and squint, it makes it even more interesting. There are sections of
dots in there that look almost like characters or symbols. Is it only my
imagination that thereís a message there somewhere?
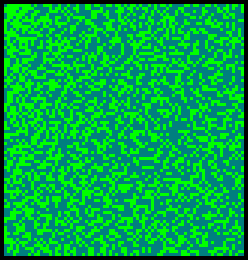
Trouble is, thereís too much
"noise" residing in the total pattern. So why donít we run this table image
through a filter of some sort to screen out the clutter? Say, we
eliminate every prime dot that doesnít have at least 3 prime
neighbors existing in the 8 cells immediately surrounding it. And maybe switch
to B&W to really try to bring those sub-images out, making the prime dots
black against white.
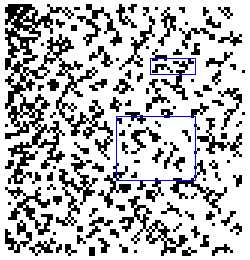
Ah-ha! There is definitely something trying to come out here. It truly is
an embedded message: the words "my" and "site". These
words have been hidden since the Big Bang
itself, buried deep within the primordial flux of pure number theory. Surely
it is a message that
God Himself, in His omniscience, created when He first numbered all the grains
of sand in our universe. A clear message that must mark this
site as something extraordinary indeed: a site favored in the eye of the
Supreme Being. Verily, all men shall marvel over this wonder, for it is
recorded here on...
Back to Prime Number Explorations...
While this article is quite obviously a parody of the current blitz of
"divine message" publications, the mathematics in it are absolutely
on the level. You can produce
the same image yourself using a starting modulo-30 prime table, collapsed to 8
"live" columns as noted above (1, 7, 11, 13, 17, 19, 23 and 29), and then
wrapping the 8-wide vertical columns after every 84 rows. Filter the resulting image
as Iíve described, and voilŗ!
Iíve wanted to do a piece on prime numbers for this site for some time, and
for some reason this "hidden message" nonsense popped into my mind when I
began to plan it. I honestly didnít know what, if anything, would turn up while
I was arranging and manipulating these prime plots. Maybe I've been focusing
so hard on my site lately, it was just meant to be!
 The
vertical compressed prime column table above reminds me an awfully lot of the
early programming card strips they used in the old
Jacquard
looms, first built about 1804. I ran into one of these antique strips one time, and its image
is shown here. Jacquard's loom was actually an improvement of an earlier
punched-card loom made by
Jacques de Vaucanson in 1745. These were the first examples of
numerically controlled (NC) machines, whose principles were later to be
adopted by the Hollerith (later IBM) Company, eventually culminating in the
modern programmable computer.
The
vertical compressed prime column table above reminds me an awfully lot of the
early programming card strips they used in the old
Jacquard
looms, first built about 1804. I ran into one of these antique strips one time, and its image
is shown here. Jacquard's loom was actually an improvement of an earlier
punched-card loom made by
Jacques de Vaucanson in 1745. These were the first examples of
numerically controlled (NC) machines, whose principles were later to be
adopted by the Hollerith (later IBM) Company, eventually culminating in the
modern programmable computer.
In my first job after graduating from college, back in 1968, I had to
program and punch out paper NC program tapes, using a special sort of
typewriter called a
Friden Flexowriter. In this case, my punched NC program strips controlled a
machine that put eyelets into printed circuit cards, giving it the x and y
coordinates to move to for each eyelet and telling it to "do its thing" at
each location. The tape looked just like the compressed prime column
table shown above. It was a fun project to work on!
The Jacquard loom program card strip was wrapped around into a continuous cylinder,
so that the pattern would repeat endlessly. I wonder what kind of fabric
weave pattern you would get by selecting some of the rows in the prime table and
making them into a Jacquard loom program? Why don't we
find out here?
See also
http://www.csicop.org/si/9711/bible-code.html#author for an interesting
article by David E Thomas on hidden text messages, insofar as they relate to
the claims purported in Michael Drosnin's 1997 book The Bible Code.
And for even more of my neurotic prime number explorations, see
here.
