In other pages on this site I played around with arranging the number
series in a 30-wide sequential table, so as to study the prime-rich columns
that derive from that particular ordering. (In order to do this effectively,
the table width Ė or modulus -- must be a multiplicand of primes: 30=2X3X5.)
You can of course also arrange the number series in other table shapes. One
interesting shape is a pyramid built from the "top down", whose descending
rows are 2 blocks wider than the previous one. The apex of the pyramid starts
at number 1. So the 2nd line is made of the numbers 2, 3, 4; the 3rd
row blocks are the numbers 5, 6, 7, 8, 9 Ė and so forth. This pyramid table
arrangement, with the prime numbers illuminated, starts off like so:
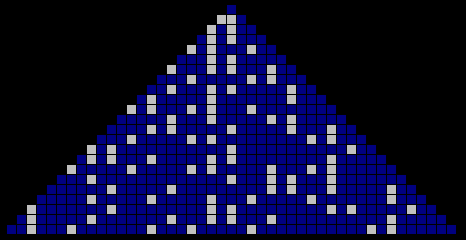
Youíll notice that the rightmost block on any row of this arrangement is
the square of the row number: 1, 4, 9, 16, 25, etc. (Count me stupid, but I
donít intuitively understand why that should be the case.) Let's look at the
prime patterns in a bigger pyramid with smaller blocks:
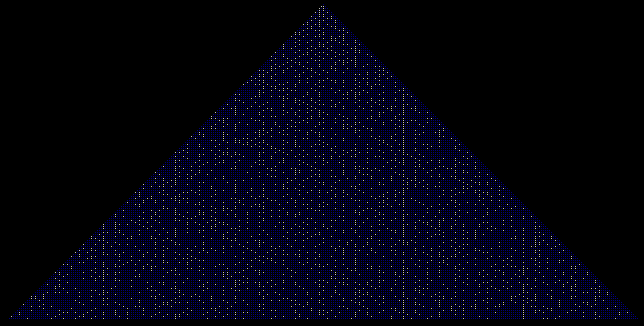
There are prime-rich columns in this pyramid, just like in my rectangular
30-wide tables. The difference is, the distribution of primes in the various
pyramid columns do not appear to be equal to each other. You can easily see
that some of the vertical columns seem to be selfishly endowed with primes at
the expense of others. There is also the appearance of diagonal prime-rich
lines.
One column to note in particular is the one starting on the right slope of
the pyramid, at 412 or 1681. Itís quite rich in primes, relative to
the other columns. Rather than starting our pyramid with the number 1, what
say we start it with 41? Here is how the patterns evolve in that arrangement:
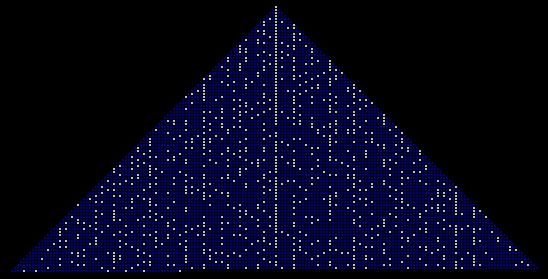
By my eyes, thatís a string of 40 consecutive primes in that center column.
I think this arrangement has some relationship to the formula N2 +
N + 41, which was known as far back as Euler to produce a rich reward of prime
numbers. (And whoís to say this knowledge was not unknown by the ancient
Egyptians when they built their pyramids?)
We can also look at prime pyramid patterns that highlight both the primes
and the "almost-primes" Ė that is, numbers that have only 2 prime factors.
That really fills out the bright spots more, and makes for more distinct
patterns and lines:

 To
the left is a thumbnail link to a bigger version. (Click your browser's
"back" button to return to this page after viewing it.) Note that same
vertical line starting at 412 (1681), now. This line doesnít seem
to want to quit being either prime, or almost-prime. I calculated the
block numbers of this vertical line down 380 rows following its starting one,
before bumping against a number with more than 2 prime factors. (It was
176861, with prime factors: 47, 53 and 71.) After this event, the line becomes
more and more typical of the other "rich" vertical lines in the "almost prime"
pyramid Ė but itís still plenty full.
To
the left is a thumbnail link to a bigger version. (Click your browser's
"back" button to return to this page after viewing it.) Note that same
vertical line starting at 412 (1681), now. This line doesnít seem
to want to quit being either prime, or almost-prime. I calculated the
block numbers of this vertical line down 380 rows following its starting one,
before bumping against a number with more than 2 prime factors. (It was
176861, with prime factors: 47, 53 and 71.) After this event, the line becomes
more and more typical of the other "rich" vertical lines in the "almost prime"
pyramid Ė but itís still plenty full.
 Like
I previously did with my rectangular number tables, we can "compress" the
columns of this prime pyramid arrangement a bit. Letís say we skip the
even-numbered ones. In other words, starting from the apex at 1, the 2nd
row of blocks is 3, 5, 7; the 3rd row is 9, 11, 13, 15, 17; and so
forth. That densifies the prime patterns quite a lot, and really brings them
out. Click the thumbnail link to the left to view this one.
Like
I previously did with my rectangular number tables, we can "compress" the
columns of this prime pyramid arrangement a bit. Letís say we skip the
even-numbered ones. In other words, starting from the apex at 1, the 2nd
row of blocks is 3, 5, 7; the 3rd row is 9, 11, 13, 15, 17; and so
forth. That densifies the prime patterns quite a lot, and really brings them
out. Click the thumbnail link to the left to view this one.
 To
the left is a thumbnail link to a bigger plot of that "compressed"
arrangement. If you search this pattern hard enough, Iíll bet you can find
your initials embedded in it somewhere!
To
the left is a thumbnail link to a bigger plot of that "compressed"
arrangement. If you search this pattern hard enough, Iíll bet you can find
your initials embedded in it somewhere!
The primes themselves are intractable beasts, but they sure do tantalize
you with hints of patterns and group order when you arrange the number series
in different ways. I've been fascinated by prime numbers for more years
than I now have left to me -- perhaps the answer to their secret will be among
my first questions to the Big Boss, after I pass that brief divide...
Back to Prime Number Explorations...
